The CAP Theorem. The Bad, the Bad, & the Ugly
The CAP theorem is too simplistic and too widely misunderstood to be of much use for characterizing systems. Therefore I ask that we retire all references to the CAP theorem, stop talking about the CAP theorem, and put the poor thing to rest
In 2000, Eric Brewer introduced the CAP Conjecture during his keynote address Towards Robust Distributed Systems at the Principles of Distributed Computing conference. Brewer posited that a distributed system cannot achieve Consistency, Availability, and Partition Tolerance simultaneously. While presented as a theorem, at that time, Brewer’s interpretation of CAP was merely conjecture, as Brewer did not offer formal proof in its support.
In 2002, Seth Gilbert and Nancy Lynch published a formal proof in Brewer’s conjecture and the feasibility of consistent, available, partition-tolerant web services, rendering their interpretation of CAP a theorem.
Since then, the CAP Theorem rose to stardom and turned into the most famous yet least useful theorem in the world of distributed systems.
CAP
The CAP Conjecture is an attempt to formulate the conflict between Consistency and Availability in the presence of Partitions while the CAP Theoremis an attempt to formalize the conflict between Consistency and Availability in the Presence of Partitions.
Informally, both the conjecture as well as the theorem define consistency as a safety property and availability as a liveness property of the system:
Consistency. Every read request receives a response indicating success and reflecting the value of the most recent write request or a response indicating failure.
Availability. Every read request receives a response indicating success (not necessarily reflecting the value of the most recent write request).
Additionally, both the conjecture as well as the theorem define a network partition as a failure mode of the underlying system model:
- Network Partition. A network partition divides the network into segments, messages sent from nodes in one segment to nodes in other segments are lost.
Formally, the conjecture and the theorem disagree about the definitions, rendering the conjecture and the theorem incomparable.
| Consistency | Availability | Partitioning | |
|---|---|---|---|
| Conjecture | Single Copy Serializability | Some node responds timely | Temporary |
| Theorem | Linearizability r/w register | Any node responds eventually | Permanent |
The conjecture doesn’t posit what the theorem proofs and the theorem doesn’t proof what the conjecture posits.
The Bad • The CAP Conjecture
Eric Brewer presented CAP as a “Pick 2 out of 3” framework. The “Pick 2 out of 3” interpretation implies that network partitions are optional, something you can opt-in or opt-out of. However, network partitions are inevitable in a realistic system model. Therefore, the ability to tolerate partitions is a non-negotiable requirement, rather than an optional attribute.
Since you have to account for network partitions, you have to choose between consistency and availability if and when a partition occurs. In other words, the CAP divides the world into CP and AP systems.
The Bad • The CAP Theorem
Seth Gilbert and Nancy Lynch published a theorem that provides a formal, mathematical articulation within the specific assumptions and constraints of their system model.
Gilbert’s and Lynch’s system model consists of three nodes, C, N₁, and N₂. Nodes do not have access to clocks and communicate by sending and receiving messages over an asynchronous network. N₁ and N₂ start out with the same value, v₀. Additionally, let’s consider a permanent network partition between N₁ and N₂. Communication is still possible between C and both N₁ and N₂, but not between N₁ and N₂.
To demonstrate the impossibility of achieving consistency, availability, and partition tolerance simultaneously, Gilbert and Lynch employed a proof by contradiction.
Assume, only for the sake of contradiction, that an algorithm exists allowing the system to be both consistent and available under this network partition.
The Algorithm’s Failure
Step 1
C sends a single write request to N₁ setting the value to v₁.
send(w, v₁) recv(w, v₁) send(ack) recv(ack)
Step 2
C sends a single read request to N₂.
send(r) recv(r) send(v₀) recv(v₀)
Under these conditions, if a write occurs on N₁ and a read occurs on N₂, the read operation will not be able to return the most recent value (v₁), thereby violating the assumed consistency.
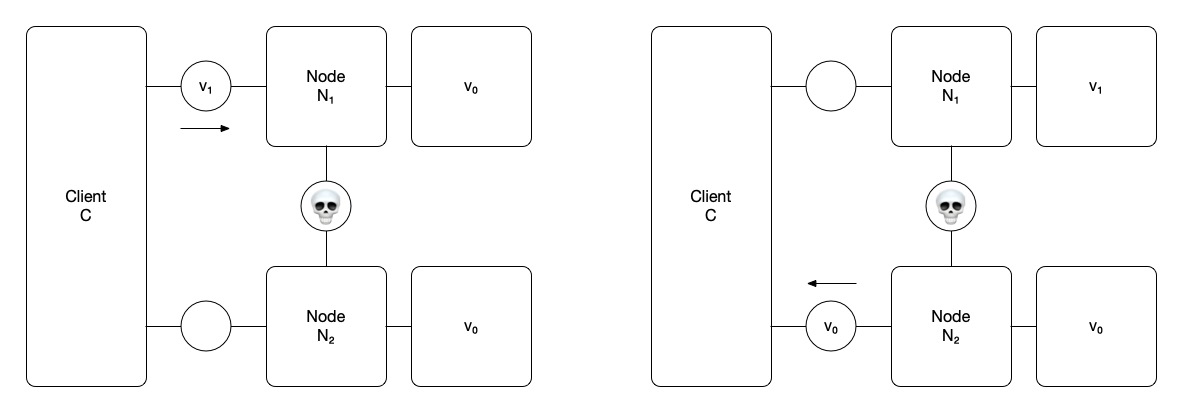
Therefore, we reach a contradiction: our initial assumption that this system could be both consistent and available is proven false.
What did this prove?!
The Ugly
The CAP theorem is often understood as demonstrating that (some further unspecified notion of) strong consistency cannot be achieved with high availability, whereas (some further unspecified notion of) weak consistency can be achieved with high availability.
However, in the case of a permanent partition, no information can flow from one segment to another. Therefore, even the weakest form of consistency is not possible in a system with a permanent partition.
On the other hand, given a non-permanent partition and the requirements that a request receives a response eventually, that is, in unbounded time, both strong consistency as well as weak consistency can be achieved.
The Ugly, Continuation
Note that Gilbert and Lynch’s definition requires any non-failed node-not just some non-failed node-to be able to generate valid responses, even if that node is isolated from other nodes. That is an unnecessary and unrealistic restriction. In essence, that restriction renders consensus protocols not highly available, because only some nodes, the nodes in the majority, are able to respond.
Consensus algorithms are all about achieving high availability while maintaining strong consistency.
Conclusion
The CAP Theorem has had both positive and negative effects on the distributed system community. On the positive side, CAP has taught us to think about the inherent trade-offs in distributed systems. However, on the negative side, CAP is often misused as a definitive argument to shut down a conversation, even when CAP may not be applicable to the design challenges at hand.
While many software engineers cite the CAP Theorem to justify their design decisions, a comprehensive understanding reveals that the CAP Theorem applies “in theory” yet may not apply to the design challenges at hand “in practice”.
Where do we go from here
The trade-offs between consistency and availablity exist, but CAP is the least useful framework to think about them. My favorite framework, Invariant confluence, is presented in the paper Coordination Avoidance in Database Systems. Invariant confluence, determines whether an application requires coordination for correct execution.
The irony of the paper referencing the CAP Theorem is not lost on me.
Receipts
- A Critique of the CAP Theorem, Martin Kleppmann
- Don’t Get Stuck in the “Con” Game, Pat Helland